$\delta (t)=\{\begin{array}{c}0\\ \infty \\ 0\end{array}\begin{array}{c}\text{for}t<0\\ \text{for}t=0\\ \text{for}t>0\end{array}\text{with}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\delta (t)}\mathrm{d}t=1$

SEE: Figure 4a) and IEC 60027-6.

Note 1 to entry: A distribution assigns a number to any function f(t), sufficiently smooth for t = t₀ [see CEI 60050-103:2009, 103-03-05].

The Dirac impulse does this according to

${\displaystyle f\left(t_0\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta }\left(t-t_0\right)f\left(t\right)\text{d}t}$.

Note 2 to entry: Any shape with area 1 may be used for the definition of δ(t), e.g. a rectangular pulse with width τ and height τ^–1, or a triangular pulse, as shown in Figure 4a), as well as a Gaussian function

${\displaystyle \frac{1}{\tau \cdot \sqrt{\pi }}\cdot e^{-\frac{t^2}{{\tau }^2}}}$.

Note 3 to entry: Any of the shapes mentioned in Note 2 to entry with τ much smaller than the smallest time constant at work in the system under consideration may be used for a technical approximation of the Dirac impulse.

Note 4 to entry: In control technology the Dirac function is mainly important for the definition of impulses and exclusively used as a function of time. Therefore the term Dirac impulse is used and the definition is adapted accordingly.

$\delta (t)=\{\begin{array}{c}0\\ \infty \\ 0\end{array}\begin{array}{c}\text{pour}t<0\\ \text{pour}t=0\\ \text{pour}t>0\end{array}\text{avec}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\delta (t)}\mathrm{d}t=1$

VOIR: Figure 4a) et CEI 60027-6.

Note 1 à l’article: Une distribution assigne un nombre à une fonction f(t), suffisamment lisse pour t = t₀ [voir CEI 60050-103:2009, 103-03-05].

L’impulsion de Dirac effectue ceci conformément à l’équation suivante

${\displaystyle f\left(t_0\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta }\left(t-t_0\right)f\left(t\right)\text{d}t}$.

Note 2 à l’article: Une forme quelconque avec la zone 1 peut être utilisée pour la définition de δ(t), ex.: une impulsion rectangulaire avec largeur τ et hauteur τ^–1, ou une impulsion triangulaire, comme indiqué dans la Figure 4a), ainsi qu’une fonction gaussienne.

${\displaystyle \frac{1}{\tau \cdot \sqrt{\pi }}\cdot e^{-\frac{t^2}{{\tau }^2}}}$.

Note 3 à l’article: Les formes mentionnées dans la Note 2 à l’article avec τ plus petit que la constante de temps la plus petite en fonctionnement dans le système étudié peuvent être utilisées pour une approximation technique de l’impulsion de Dirac.

Note 4 à l'article: Dans la technologie de commande, la fonction de Dirac est principalement importante pour la définition des impulsions et est exclusivement utilisée comme fonction de temps. Par conséquent, le terme d’impulsion de Dirac est utilisé et la définition est adaptée en conséquence.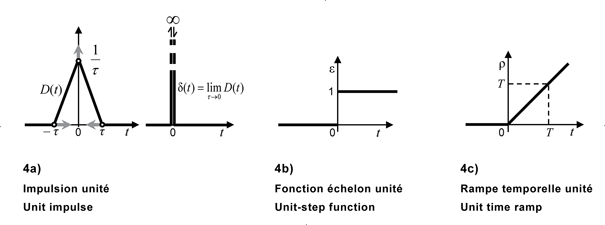

Figure 4 – Unit test functions

Figure 4 – Fonctions du test unités