Note 1 to entry: From a mother wavelet ${\displaystyle \psi (t)}$, daughter wavelets are obtained through shifting and scaling (expansion or compression): ${\displaystyle {\psi }_{a,b}(t)=\frac{1}{\sqrt{a}}\psi \left(\frac{t-b}{a}\right)}$, where a is a scale parameter and b a position parameter.

Note 2 to entry: Examples (see Figures 3 and 4):

• Haar wavelet: ${\displaystyle \psi (t)=-1}$ for −1/2 < t < 0, ${\displaystyle \psi (t)=1}$ for 0 < t < 1/2, ${\displaystyle \psi (t)=0}$ outside;
• Morlet wavelet: ${\displaystyle \psi (t)={\mathrm{e}}^{-t^2/2}{\mathrm{e}}^{-\mathrm{j}\omega t}}$ (example of exponential damping; Figure 4 gives the real part).

Figure 3 – Haar wavelet

Figure 3 – Ondelette de Haar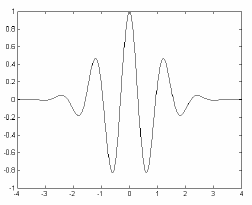

Figure 4 – Morlet wavelet

Figure 4 – Ondelette de Morlet