Note 1 to entry: The Dirac function can be considered as the limit of a function, equal to zero outside a small interval containing the origin, and the integral of which remains equal to unity when this interval tends to zero. See Figure 1, where instead of a triangle any other shape with area 1 is possible, too.

Note 2 to entry: The Dirac function is the derivative of the unit step function considered as a distribution.

Note 3 to entry: The Dirac function can be defined for any value x₀ of the variable x. The usual notation is: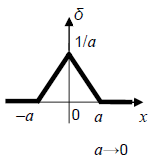

$f(x_0)={\displaystyle {\int }_{-\infty }^{+\infty }\delta (x-x_0})f(x)\mathrm{d}x$

Figure 1 – Dirac function